【問題2】 次の直角三角形について,指定された三角比の値を求めてください.(選択肢の中から正しいものをクリック)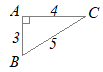 (1)
(1) |
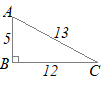 (2)
(2) |
【問題2】 次の直角三角形について,指定された三角比の値を求めてください.(選択肢の中から正しいものをクリック) (1)
(1) |
 (2)
(2) |
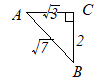 (3)
(3) |
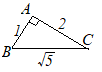 (4)
(4) |
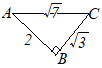 (5)
(5) |
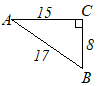 (6)
(6) |
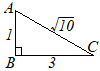 (7)
(7) |
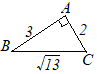 (8)
(8) |
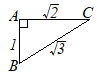 (9)
(9) |
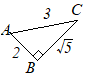 (10)
(10) |
|
#危険な落とし穴に注意# 直角三角形の辺の長さの比は三角比になりますが,直角三角形でなければ,辺の長さの比が三角比になるとは限りません. すなわち,「辺の長さの比」が三角比になるのは,直角三角形の場合だけです.このことを忘れると大変なことになります!!! 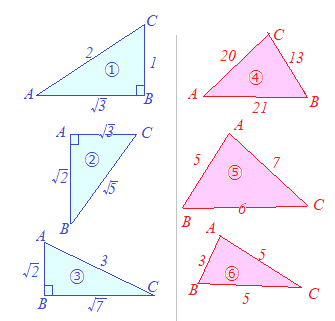 上の図で,左側に描いた水色の三角形は「直角三角形」だから,その辺の長さの比は三角比になります.
上の図で,左側に描いた水色の三角形は「直角三角形」だから,その辺の長さの比は三角比になります.
【例】
しかし,右側に描いた桃色の三角形は「直角三角形ではない」ので,辺の長さの比がそのままで三角比にはなりません.
図①で, 図②で,
【例】
※それなら,例えば図④の図④で, 図⑤で, ⇒ 次の図のように「直角三角形」を描いて, 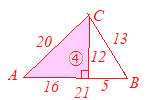 |
|
■[個別の頁からの質問に対する回答][基本的な三角比の値(図あり)について/16.11.13]
もっと問題を増やしてほしいです。
■[個別の頁からの質問に対する回答][基本的な三角比(図あり)について/17.4.3]
=>[作者]:連絡ありがとう.三角比の入門で取り扱う角度は全部で3個で三角関数の種類が3種類なので,合計9個ですべての問題を網羅しています.だからその項目ではそれ以上問題を増やすことはできません. その頁が済んだら,先頭のサブメニューに沿って,図なしに進み,さらにその次の項目を目指してください. なるほど!分かりました
こんなにいろいろ作ってお疲れ様です
=>[作者]:連絡ありがとう. |