maximaの初歩的な操作15･･･２次元グラフの描き方

== maximaの初歩的な操作15･･･２次元グラフの描き方 == ○Xmaxima，wxMaxima のインストール方法，基本操作については［この頁］参照

○wxMaximaで２次元グラフを描くには
メニューから［プロット］→［２次元プロット］を選ぶと，対話型記入欄になるので
関数，変数，x座標の区間を入力し，ＯＫボタンを押す．

○入力に当たっては，2xなどの書き慣れた記号を2*xと書かなければならないことに注意しましょう．べき乗（指数）を2^nなどと書くのは，TeXの書き方とほぼ同じ

【wxMaximaで２次元グラフを描くには】

［例１］
$y=x^2$ のグラフを描くには

メニューから［プロット］→［２次元プロット］を選ぶと
対話型記入欄が出てくるので，次の図の青字で示した項目を埋めて，他の項目はそのままにしてＯＫボタンを押します．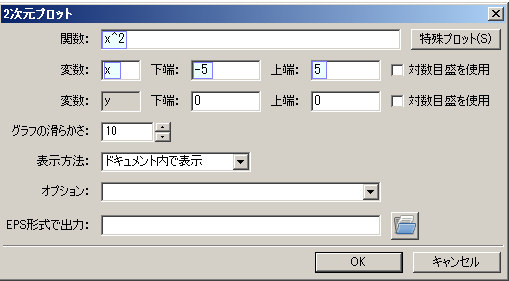

≪結果≫
　次のようなグラフが描かれます．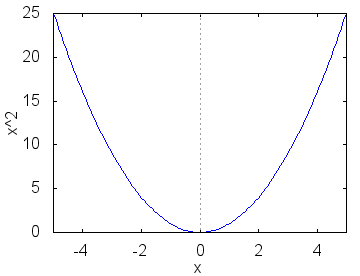

≪参考≫

(1)　この描き方では，関数の項目にy=x^2などと記入するのではなく，
その右辺の関数x^2だけを記入することが重要です．

2)　wxMaximaの対話型記入欄をたどれば，自動的に
wxplot2d([x^2], [x,-5,5])$
のように必要事項が書き込まれますが，これが直接入力するときの関数と引数を表しています．
　すなわち，
wxplot2d([関数], [変数,変数の下端,変数の上端])$
の形で入力します．行末のドルマーク＄はセミコロン；でもよく，Shift+Enterで実行するときはそれも略してよい．

　maximaで関数の引数に［　］のように書かれているところは，配列が入るようになっていて，このwxplot2d([関数], ...)において関数の部分はカンマで区切って複数個の関数を並べることでできます．次の［例２］でこれを示します．

(3)　変数xの下端と上端に指定した範囲のグラフが描かれ，「y方向はその区間の最小値から最大値まで拡大または縮小して」示されますので

1)　縦横の縮尺比は１：１とは限りません．
2)　その区間でのyの最小値・最大値によって，縦方向の表示が引きずられるので，自分が調べたいグラフの特徴が表示できるようにするには，下端と上端を調整する必要があります．

変数yの欄が灰色表示になっていて，下端０，上端０になっているところを，今の場合−5≦x≦5に合わせて−5≦y≦5とすると「縦横比がそこそこ一致します」…そこそこというのは，描画画面自体が正方形でなく縦3：横4の長方形になっているので，正味の１：１にするには−4≦x≦4 , −3≦y≦3などとしなければならないということです．
　直接入力でこれを行うには，x の値の範囲， y の値の範囲を次のように配列として並べるとよい．
wxplot2d([x^2], [x,-4,4], [y,-3,3]);

［例２］
$y=\sin x$ ， $y=\cos x$ ， $(0\leq x \leq 2\pi)$ のグラフを重ねて描くには

メニューから［プロット］→［２次元プロット］を選び，対話型記入欄の関数の欄に
sin(x),cos(x)のようにカンマで区切って２つの関数を書き込みます．
変数の下端は０とし，上端は2*%piとします．
他の項目はそのままにしてＯＫボタンを押します．

≪結果≫
入力コマンドが次のように入ります．
wxplot2d([sin(x),cos(x)], [x,0,2*%pi])$
　次のようなグラフが描かれます．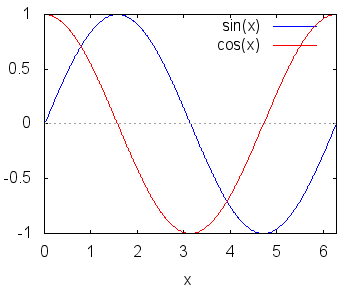

［例３］
　媒介変数表示で楕円
$x=2\cos t$ ， $y=3\sin t$ ， $(0\leq x \leq 2\pi)$ のグラフを描くには

≪入力≫
　直接入力するには (%inn) の行に
wxplot2d([['parametric, 2*cos(t), 3*sin(t), [t, 0, 2*%pi], [nticks, 300]]], [x,-5,5])$
などと記入しなければならないが，これを覚える必要はない．
　メニューから［プロット］→［２次元プロット］を選び，対話型記入欄において
関数の右にある［特殊プロット］→［媒介変数プロット］を選ぶと，次のような入力欄が現れる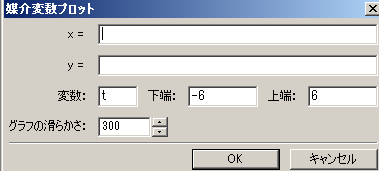

　下の欄に変数としてtが書き込まれているので，これをそのまま使うには媒介変数をtとしてx , yの式を書き込む．媒介変数に他の変数を使うときは，下の欄の変数も書き換える．
x=2*cos(t)
y=3*sin(t)
変数 t の下端0上端2*%pi
を書き込んでＯＫボタンを押し，さらにもう１つのＯＫボタンを押すと次のようなグラフが描かれる．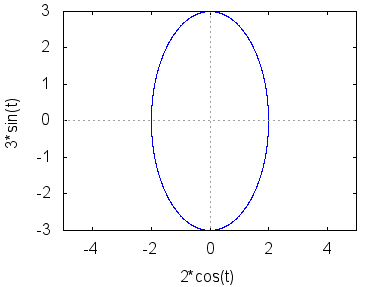

　このグラフは縦横比が１：１でないので，これを１：１にするには，前期の x の値の範囲を −3 から 3 に書き換えればよい．
すでに表示されている (%inn) の欄を
wxplot2d([['parametric, 2*cos(t), 3*sin(t), [t, 0, 2*%pi], [nticks, 300]]], [x,-3,3])$
に書き換えるか，または，先ほどの対話型記入欄においてx の値の範囲を −3 から 3 に書き換えてからＯＫを押せばよい．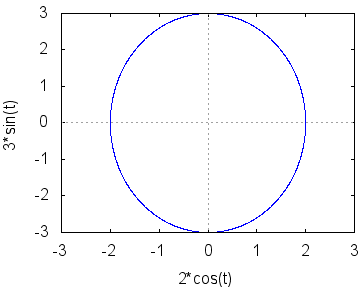

【得られたグラフを画像ファイルとして保存するには】
　２次元グラフを作成する対話型記入欄の中で［EPS形式で出力］という項目を選ぶこともできるが，画像ファイルによってはEPS形に対応していない場合もあるので，むしろ単純に画面に表示されたグラフを右クリックして［画像として保存］を選べば，PNG , JPG, GIFなどの画像形式で保存できる．

【グラフの滑らかさの指定とは】
　２次元グラフを作成する対話型記入欄の中に［グラフの滑らかさ］という項目があります．コンピュータによる曲線の描画は，点をつないだ折れ線として示されますが，これを計算するときの点の数に関係しているようです．大きな整数を与えるほど滑らかになることになっていますが，通常は既定値で書き込まれている値のままで十分です．100倍してもたいして変わりません．ただし，この値（nticks というパラメータの値になる）を1とか2のような極端に小さな値にすると角のある折れ線になります．

［例４］
　陰関数表示で楕円
$\frac{(x-1)^2}{9}+ \frac{(y-2)^2}{4}=1$
のグラフを描くには

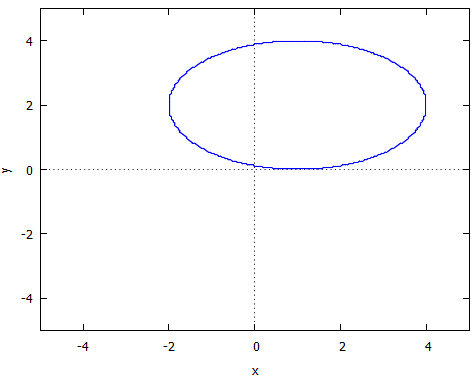
　メニュー画面から選択する方法はなさそうなので，次のように (%inn) の行に直接入力します．（他にも方法はありますが，初歩的にはこの方法が分かりやすい）
≪入力≫

陰関数表示のパッケージをロードする
(%inn) load(implicit_plot);
次の関数を実行する
(%inn) implicit_plot((x-1)^2/9+(y-2)^2/4=1,[x,-5,5],[y,-5,5]);

≪結果≫

　別ウィンドウが開いて次のようなグラフが表示されます．

...メニューに戻る　

..maximaのメニューに戻る