.

■信頼性係数の計算

○　ExcelからRコマンダーを用いて信頼性係数を求めるには
  1. RExcel→ｓｔａｒｔ R（しばらく待つ）［小さなウィンドウが１つ開くがそのままにしておく］
  2. RExcel→RCommander→with separate menus［小さなウィンドウがもう一つ開く］
  3. （以下Rコマンダーのメニューで）データ→データのインポート→ExcelまたはAccess，dBaseのデータセットから
  4. データセット名を入力→（通常はそのままで）OK
  5. Excelファイルが保存されているフォルダ，ファイル名を選ぶ→開く
  6. Excelファイルには通常複数のシートがあるので，どのシートをインポートするのかを選ぶ→ＯＫ（ここで意図したとおりのデータがインポートされているかどうかを［データセットを表示］ボタンで確かめるとよい［小さなウィンドウがさらに１つ開くが，これはそのままでもよいし，確認後閉じてもよい］）
  7. 統計量→次元解析→スケールの信頼性..→（変数３つ以上を選択のメニューが出る）比較したい項目をすべて選択する（Ｓｈｉｆｔキーを押しながらすべて反転表示にする）→ＯＫ
  8. 右の表１のような出力が得られる．（p1〜p10はこのデータの列表題）
  9. 出力結果をテキストファイルに保存するには，ファイル→出力結果をファイルに保存
(*1)　RおよびRコマンダーのインストール方法については別途参照

(*2)　ExcelファイルをRにインポートする方法については別途参照・・・なお，Excelファイルは複数のシートから成っていてもよいが，インポートすべきシートにおいてはセルA1から行方向に列のラベルが並んでいて，行のラベルはない方が失敗しにくい．特に下の表２のようにＡ列にデータの整理番号などの「数字からなるラベル」があると他のデータと混乱しやすいので注意
表1
Alpha reliability = 0.7753
Standardized alpha = 0.7758

Reliability deleting each item in turn:
Alpha Std.Alpha r(item, total)
p1 0.7745 0.7766 0.2791
p2 0.7665 0.7668 0.3563
p3 0.7573 0.7556 0.4437
p4 0.749 0.7469 0.5079
p5 0.7543 0.7546 0.4575
p6 0.7354 0.7367 0.591
p7 0.7463 0.7485 0.5128
p8 0.7466 0.7492 0.5126
p9 0.7826 0.7812 0.2569
p10 0.746 0.7487 0.5159
■出力結果が表す内容
○　信頼性係数とは
　テスト結果の内部的一貫性を示す信頼性係数という指標は古典的テスト理論の重要な成果の１つだと言われている．
　同じテストを繰り返し行ったときに同じ結果が得られるかどうか，すなわち再現性を調べたいときに同じ条件で何度もテストを行うのは困難なことが多いので，１回のテストから得られたデータを統計的に処理することによってこれを推定していく手法として考案されたもの．
　中でもスピアマン・ブラウンの公式，クロンバックのα係数が有名である．		 　
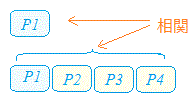
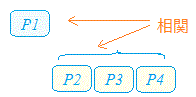
○　I-T相関，I-R相関とは
　テスト項目・質問項目が幾つかあるとき（表1ではp1〜p10まで10項目となっている），各項目の得点(item score)と合計得点(total score)との相関係数が高いときには，各項目で測定されている内容とテスト全体で測定されている内容の一貫性・整合性が高いと考えることができる．
　そこで，各項目と合計得点との相関係数をその項目の信頼性の指標として用いるのが項目-テスト相関（Ｉ−Ｔ相関）である．
　ところが，合計得点にはその項目の得点も含まれているため項目数が全部で３，４項目というように少ないときにＩ−Ｔ相関を用いると実態以上に高くなりやすい．
　そこで，各項目（item score）とその項目を除いた残りの項目の合計得点（remainder score）との相関係数（I-R相関）を用いるとその項目の得点が含まれるのを防ぐことができる．もちろん，項目数が多いときにもI-R相関を計算してもよく，常にI-R相関で計算すると決めておくと基準がはっきりして比較しやすくなる．
　Rコマンダーにおいて「Reliability deleting each item in turn：各項目を順に取り除いた信頼性係数」と書かれているのは，その項目を除いたものとの関係であることを示している．
　表１の（項目名を第１列とするとき）第４列に表示されているのがこのI-R相関になっている．		 I-T相関

I-R相関

※ＩｰR相関の値と信頼性の目安について書かれた書物をなかなか見つけられないが，筆者の行ったテストでは高いときは0.7〜0.8程度，低いときは0.3程度の値になることがある．
○　クロンバックのα係数（信頼性係数）とは
　右のような４項目のテスト結果について，合計得点のばらつき（分散0.977）は「各項目ごとのばらつき」（項目ごとに計算した分散の和0.425）と「全体に共通のばらつき」から成り立っていると考えると，
によって求められる量がこれらの項目全体によって測定された得点の一貫性・整合性と考える．ただし，標本の分散から母集団の分散を推定するときにN/(N-1)を掛けて不偏推定値を求めるのと同様にN/(N-1)を掛けた値を用いる．（Nは項目数）
･･･（Ａ）
　右の例ではα=4/3*(1-0.425/0.977)=0.753となる．
　表1においてはAlpha reliability = 0.7753がこれを表している．
　統計においては，元のデータを加工した標準化データ（各データから平均値を引いて標準偏差で割ったもの）が用いられることが多く，標準化データから出発したときの信頼性係数がStandardized alpha = 0.7758として示されている．
表２
　 p1 p2 p3 p4 計
No.1 0.94 0.83 0.56 0.21 2.54
No.2 0.12 0.24 0.3 0.12 0.78
No.3 0.92 0.86 0.72 0.41 2.91
No.4 0.09 0.16 0.72 0.05 1.02
No.5 0.23 0.31 0.42 0.11 1.07
No.6 0.83 0.27 0.14 0.91 2.15
No.7 0.62 0.55 0.38 0.56 2.11
No.8 0.83 0.76 0.96 0.99 3.54
分散 0.135 0.083 0.071 0.136 　
　 　 　 和→ 0.425 0.977

※クロンバックのα係数が0.8程度ならば十分な一貫性があり，0.7程度でもそこそこ・まあまあの一貫性があると考えられている．
※一般に，項目数が増えるとα係数は高くなるとされている．
　（Ａ）で定義されるクロンバックのα係数（通常単に信頼性係数といえばこれを指すことが多い）は項目全体の信頼性を１つの小数で表している．したがって，各項目ごとの信頼性はこれだけでは分からないので，「全体の信頼性係数と各項目を順に取り除いた残りの項目の信頼性係数を比較して，残りの項目の信頼性係数の方が格段に高ければその項目は信頼性が低く集計に含めない方がよい」という形で判断材料が提供されることになる．
　「Reliability deleting each item in turn：各項目を順に取り除いた信頼性係数」と書かれた表の第2列はその項目を取り除いたときの残りの項目の信頼性係数，第3列は標準化データを用いたときの値を表している．		 ※以上の結果を踏まえて表1の出力結果をもう一度見てみると
　上の表１においてp9の項目はI-R相関が低く，α係数もp9を取り除いたときの方がよくなっている．
　通常，項目数が多いほどα係数は高くなるはずであるが，項目数を減らしているのにα係数が高くなるというのは，この項目による測定の信頼性に疑問があることになる･･･実際には，この項目はよく考えなければ答えられないはずの問題を４択にして先頭の選択肢を解答にしたもので，当て推量（まぐれ当たり）が数多く発生した可能性があり，これが信頼性係数に反映していると考えられる．
⇒表1においてp9の信頼性は疑問であると判断できる．
...メニューに戻る　..Rのメニューに戻る
■［個別の頁からの質問に対する回答］[信頼性係数の計算について／18.9.10］
統計は初心者なので、とても難しくとらえていますが、そんな私にもわかりやすい内容でした。 ありがとうございます。
＝＞［作者］：連絡ありがとう．